回归分析中的“回归

**一、一些前置知识**
------------

[回归分析][1]是研究自变量与因变量之间数量变化关系的一种分析方法，它主要是通过构建因变量[Y][2]与影响它的自变量X之间的[回归模型][3]衡量自变量X对因变量Y的影响能力，进而可以用来预测因变量Y的发展趋势。

可以简单理解为，我们希望通过X去发现或预测Y的变化规律，这里的X既可以是一个影响因素也可以是多个影响因素。一个时即为一元回归，多个时即为[多元回归][4]。

存在线性关系则为[线性回归][5]，存在[非线性][6]关系则为[非线性回归][7]。如果用一个基础性的表达式表示：

Y=f(X)+ε

Y：因变量（也称为[被解释变量][8]）

X：自变量（也称为解释变量）

ε：[误差项][9]

f(·)：根据回归模型的类别不同而结构不同

**二、线性回归**
----------

### 1.一元线性回归

![](/upload/turndown-pics/20240401/v2-7cdc738d09c7645920f939636aded2d5_720w.png?source=2c26e567)

广告是企业自我宣传或增值的有效方式，通过广告投入，可以提升品牌知名度、创造消费者需求、促进重复购买，提升销售能力。那到底广告费用与销售额存在着怎样的定量关系？

**STEP1：绘制[散点图]初步观察广告费用与销售额的关系**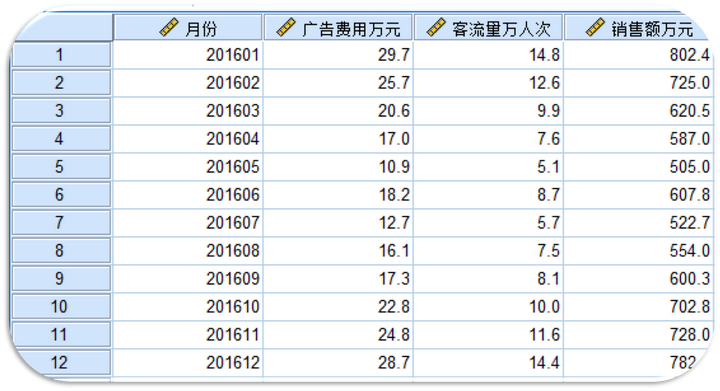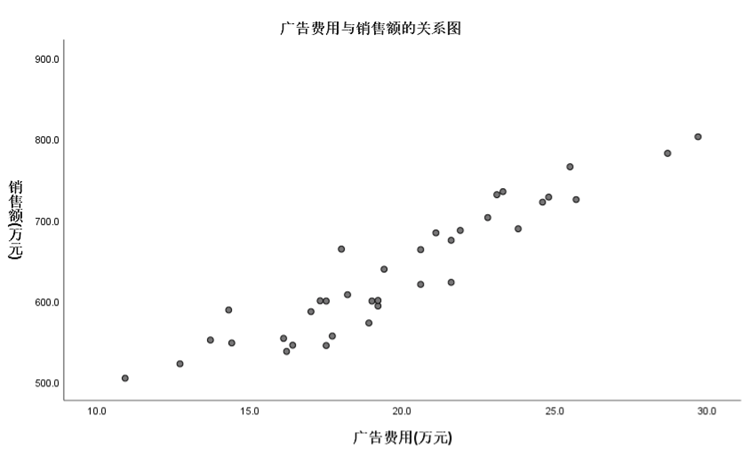

![](/upload/turndown-pics/20240401/v2-0f20aae59f0f318b3176036e8c4e20fa_720w.png?source=2c26e567)

![](/upload/turndown-pics/20240401/v2-01515253631293a0bcc021a771d7c551_720w.png?source=2c26e567)

**STEP2：从图中可以发现广告费用与销售额存在着线性正相关关系。**

**可以采用[一元线性回归模型]来探索规律。**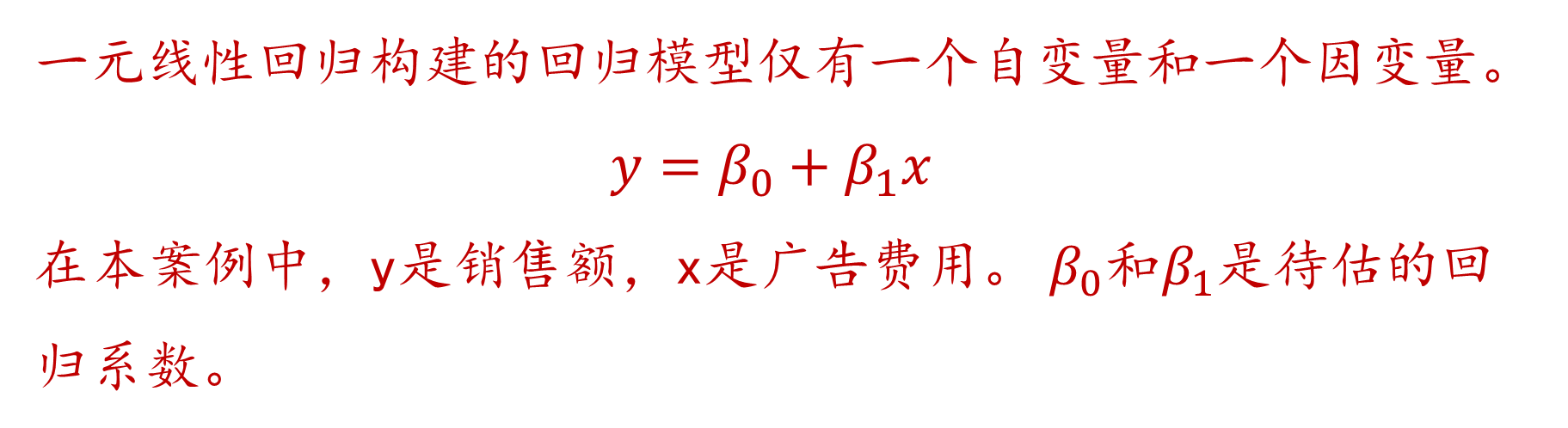

![](/upload/turndown-pics/20240401/v2-6b4fabd8a70bf0433f953e596a838bc2_720w.png?source=2c26e567)

**STEP3：SPSS中计算**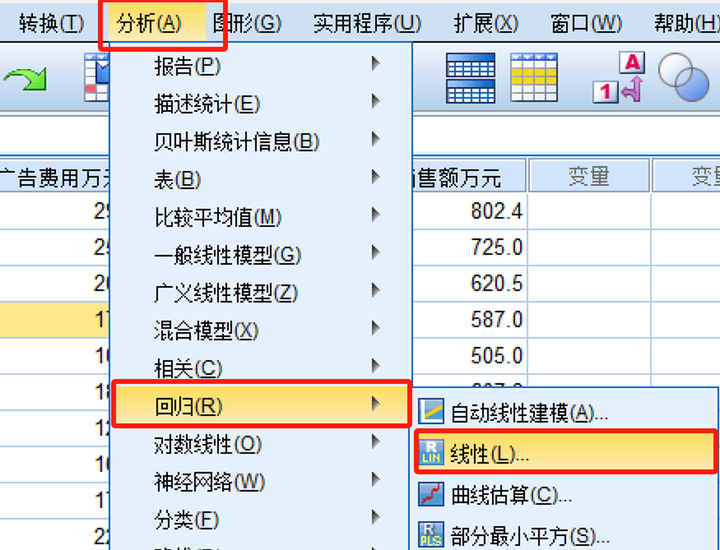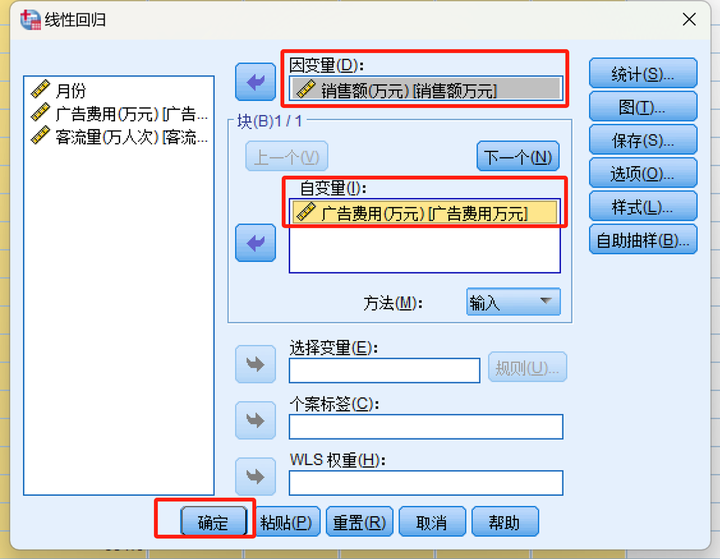

![](/upload/turndown-pics/20240401/v2-e6056957f24801ed227f39d2a06dccd0_720w.png?source=2c26e567)

![](/upload/turndown-pics/20240401/v2-29fc3b485cfafd8091455a75b90713ed_720w.png?source=2c26e567)

**STEP4：解读结果——重点看四处**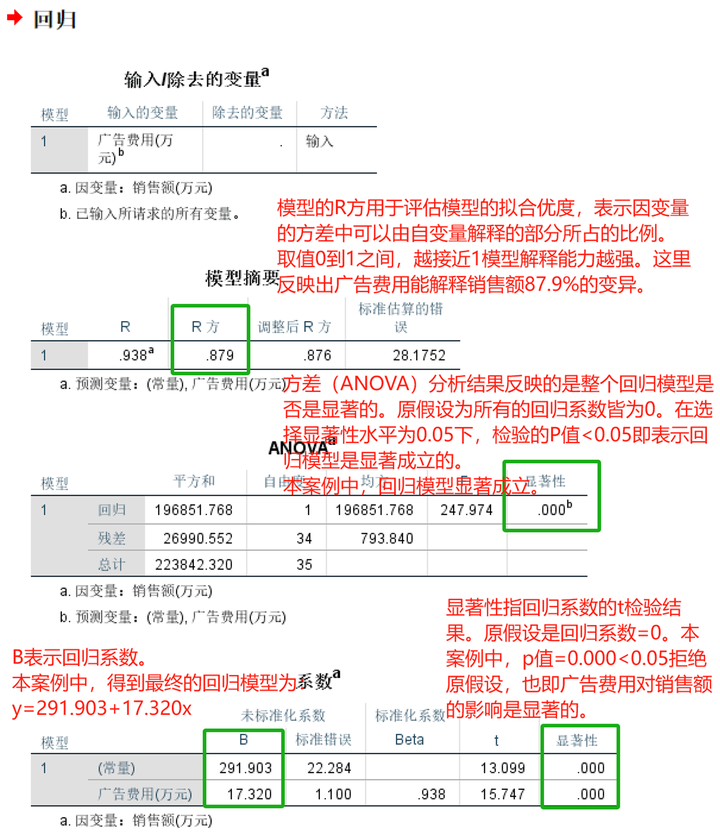

![](/upload/turndown-pics/20240401/v2-623cf52b51e2e7d1954998979cc631e1_720w.png?source=2c26e567)

**STEP5：应用模型**

y\=291.903+17.320xy=291.903+17.320xy=291.903+17.320x

①解释二者的影响关系

[回归系数]展示的是自变量对因变量的影响方向和程度。自变量每变化一个单位，平均来说因变量增加/减少回归系数个单位。常量不用解释。

本案例中，广告投入是销售额的正向影响因素。广告费用每增加1万元，销售额平均来说增加17.32万元。

②预测

将自变量/因变量已知值带入回归模型，即能预测因变量/自变量的值。

比如，下个月该公司的广告费用预计将投入20万元，则销售额预计能达到：

291.903+17.320\*20=638.303（万元）

比如，下个月该公司计划销售额目标为800万元，广告费用应投入多少万元？

(800-291.903)/17.320=29.336（万元）

### 2.多元线性回归

除了广告费用外，销售额还与很多因素有关，其中一个紧密的相关因素就是客流量。

接下来，我们考虑广告费用和客流量两个影响因素，分析销售额。

多个变量构建线性回归模型即为[多元线性回归][14]。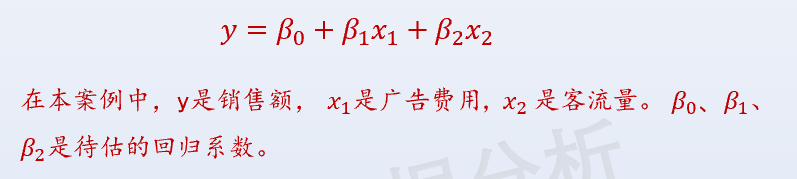

![](/upload/turndown-pics/20240401/v2-c99dacb360b295932a8d74e3848234d9_720w.png?source=2c26e567)

**SPSS操作：**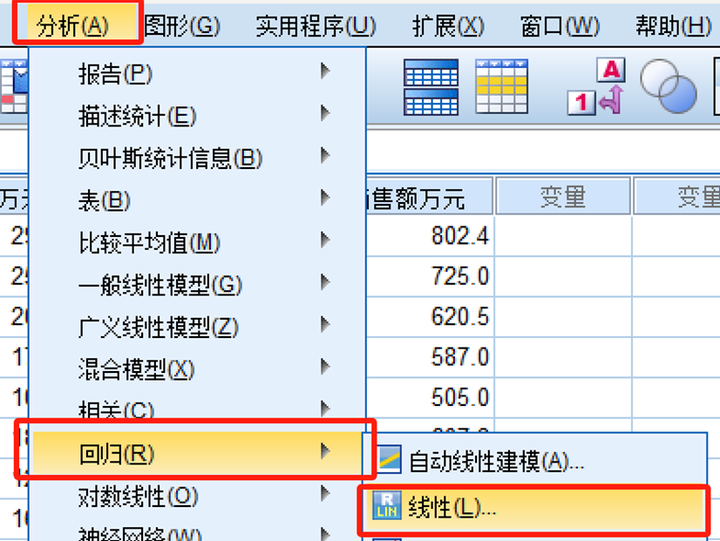

![](/upload/turndown-pics/20240401/v2-dce3667435dd0d5dd2552999fd9c1d1b_720w.png?source=2c26e567)

![](/upload/turndown-pics/20240401/v2-1a706a6fe76b50c6514822db27e5c835_720w.png?source=2c26e567)

**解读结果，重点看四处：**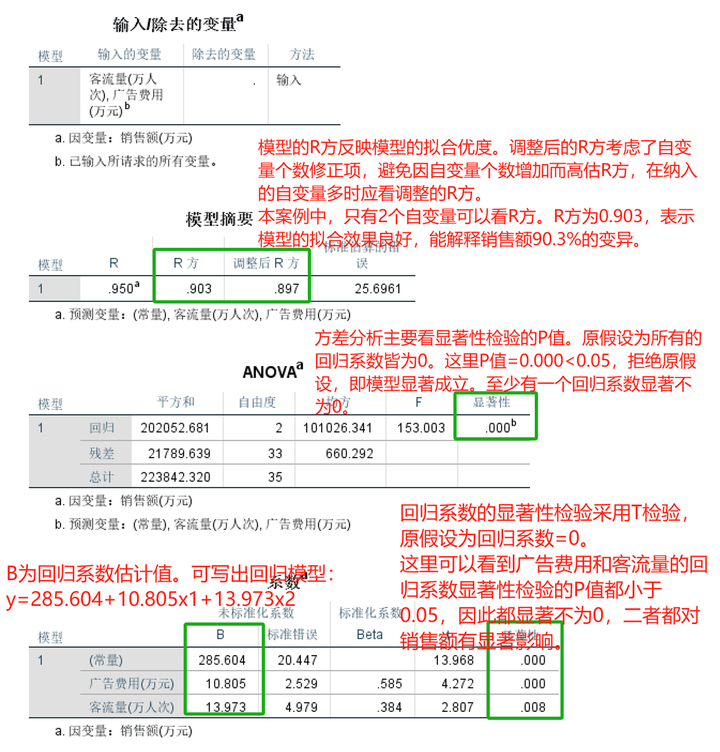

![](/upload/turndown-pics/20240401/v2-6bcc629b3593a7b2eee613f1e7af5dad_720w.png?source=2c26e567)

**应用模型**

![](/upload/turndown-pics/20240401/v2-96a00635ab8aaf460297887435af0784_720w.png?source=2c26e567)

①解释二者的影响关系

回归系数展示的是自变量对因变量的影响方向和程度。在其他自变量不变情况下，当前自变量每变化一个单位，平均来说因变量增加/减少回归系数个单位。常量不用解释。

本案例中，广告投入和客流量均是销售额的正向影响因素。在客流量不变的情况下，广告费用每增加1万元，销售额平均来说增加10.805万元；在广告费用不变的情况下，客流量每增加1万人次，销售额平均来说增加13.973万元。

②预测

将自变量/因变量已知值带入回归模型，即能预测因变量/自变量的值。

比如，下个月该公司的广告费用预计将投入20万元，客流量预计能达到10万人次，则销售额预计能达到：

285.604+10.805\*20+13.973\*10 = 641.434（万元）

比如，下个月该公司计划销售额目标为800万元，客流量预计达到11万人次，广告费用应投入多少万元？

(800-285.604-13.973\*11)/10.805 = 33.382（万元）

2024-04-01 21:33 by admin 94 0

注：本文转载自https://www.zhihu.com/question/30123729/answer/3383961003，如有侵权行为，请联系我们，我们会及时删除。

回归分析中的“回归

热门文章